[Theory of Computation] 계산이론(2강) - Automata의 시작, DFA

• 수식이 제대로 보이지 않는다면, 새로고침(F5)을 해주시기 바랍니다.
• 참고 교재: An Introduction to Formal Languages And Automata(Peter Linz)

Automata

오토마타(Automata)는 추상적인 연산 장치를 의미합니다. 쉽게 생각하면 컴퓨터를 생각하시면 됩니다. 물론 Automata가 실제 물리적인 기계 장치만을 의미하지만은 않습니다. 계산 할 수 있는 추상적인 연산 장치로 생각하시면 될 것 같습니다. 그리고 ‘연산 장치가 계산을 할 수 있는가? 할 수 없는가?’를 다루는 학문이 계산 이론입니다.

Deterministic Finite Automata(DFA)

DFA의 정의는 다음과 같습니다.
M is DFA, defined by 5-tuples, \(M=(Q, \Sigma, \delta, q_0, F)\)
이렇게만 봐서는 당연히 이해가 안됩니다. \(Q\)부터 \(F\)까지 의미를 하나씩 살펴봅시다.
아래에 DFA의 예시인 그림이 있으니, 설명과 그림을 동시에 참고하시길 바랍니다.
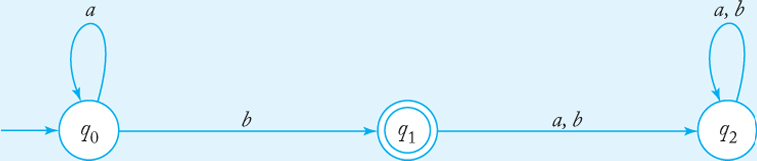
\(Q\)는 states들의 집합을 의미합니다. 그림에서는 즉, \(Q\)의 원소는 \(q_0, q_1, q_2\)가 됩니다.
\(\Sigma\)는 지난 강의에서 설명한 의미와 동일합니다. 즉, symbols들의 집합입니다. 아래 그림에서는 a, b가 되겠습니다.
\(\delta\)는 transition function을 의미합니다. \(\delta(currentState, symbol)\)의 형식으로 표기합니다. 예를 들어 아래 그림에서는 \(q_0\)에서 $b$를 소모하여 \(q_1\)으로 이동할 수 있으므로 \(\delta\)에는 \(\delta(q_0, b)\)가 포함되어 있습니다. 이런 식으로 모든 경로에 대하여 transition function을 가집니다.
$q_0$는 initial state, $F$는 final state들의 집합을 의미합니다. initial state는 반드시 하나지만, final state는 여러 개 존재할 수 있습니다. 따라서 $q_0$는 element, $F$는 set의 개념입니다.

또한 정말 중요한 특징이 하나 있는데요, 각 state에서 다른 state로 가리키는 화살표가 symbol당 반드시 하나씩! 존재해야 한다는 특징이 있습니다. 그림을 보시면 각 state에서 빠져나오는 화살표가 모두 2개씩 있고, a, b 각각 하나씩 차지합니다. 매우 중요하니 꼭 기억하시길 바랍니다. NFA에 대해서 미리 말씀드리자면, DFA에서 이 규칙이 깨지면 NFA가 됩니다.

그래프의 노드에 해당하는 부분\((q_0, q_1, q_2)\)이 state를 나타냅니다. 동그라미가 두 개 그려진 노드\((q_1)\)가 final state에 해당됩니다. 어떤 string이 이 DFA를 통과하여서 모든 symbol들을 소모하고 끝났을 때 위치가 final state를 통과한다면, 이 DFA를 만족하는 Language에 포함된 string으로 볼 수 있습니다.
굉장히 중요한 개념이지만, 처음에는 헷갈릴 수 있습니다. 예시를 보시면 바로 이해하실 수 있을 것 같습니다.
string이 “ab”라고 가정해봅시다. 처음 \(q_0\)로 간 후, $a$를 소모하여 \(q_0\)로 갑니다. 그리고 \(b\)를 소모하여 \(q_1\)에 도착하게 됩니다. 모든 symbol을 사용하였고, final state에서 끝났기 때문에 “ab”는 이 DFA가 표현하는 Language에 포함된 string인 것입니다. 반면 string “a”는 \(q_0\)에서 끝나기 때문에 이 Language 안에 존재하지 않습니다.
또한 DFA를 만족하는 string들을 몽땅 모든 Language가 있을 때, \(L(M) = \{\, w \in \Sigma^* : \delta^*(q_0, w) \in F \,\}.\)라고 표현합니다.

Example

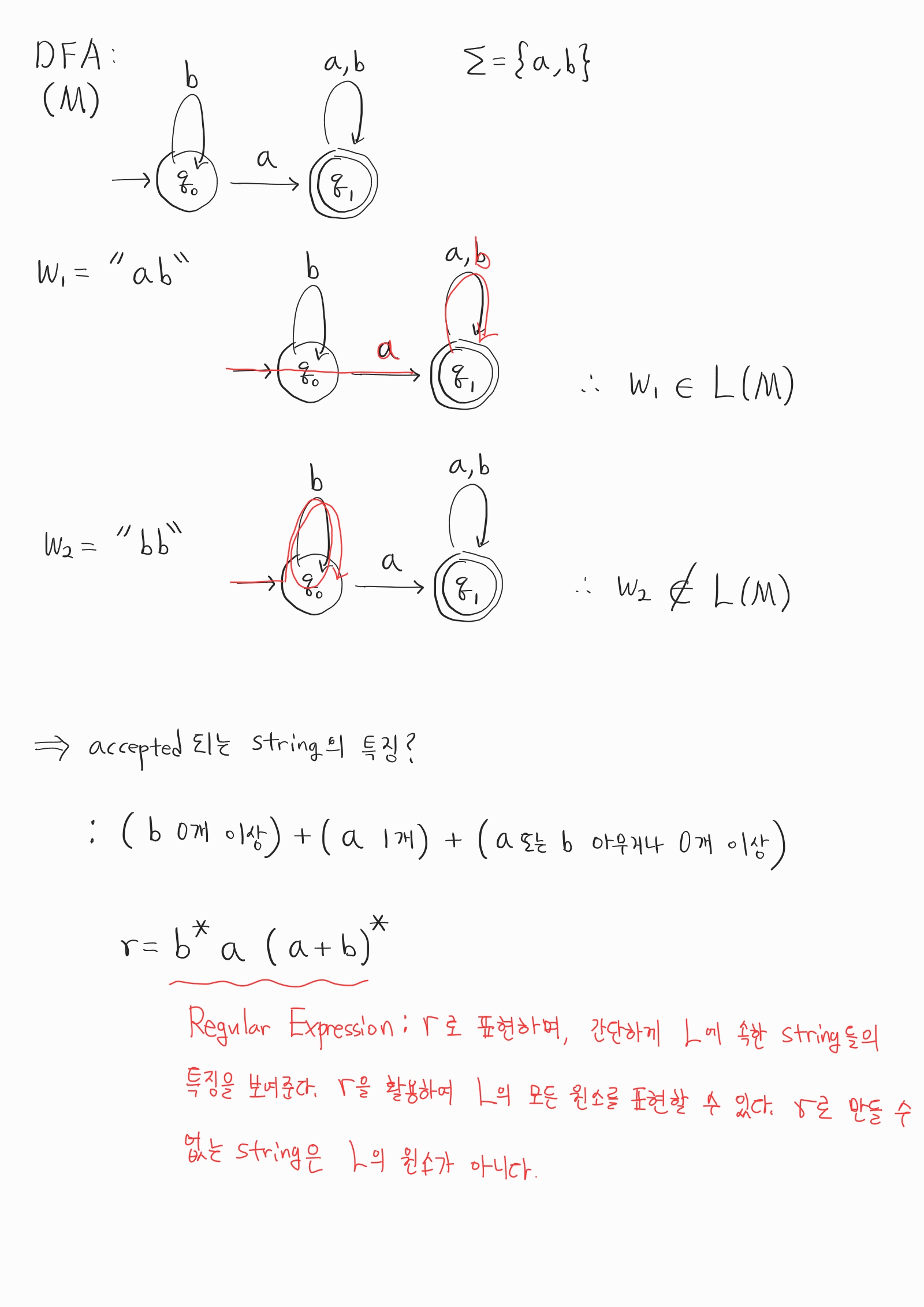
더 많은 예시를 보여드리고 싶은데, 글자만으로는 설명에 한계가 있는 것 같아서 그림을 통해 함께 알아보도록 합시다.
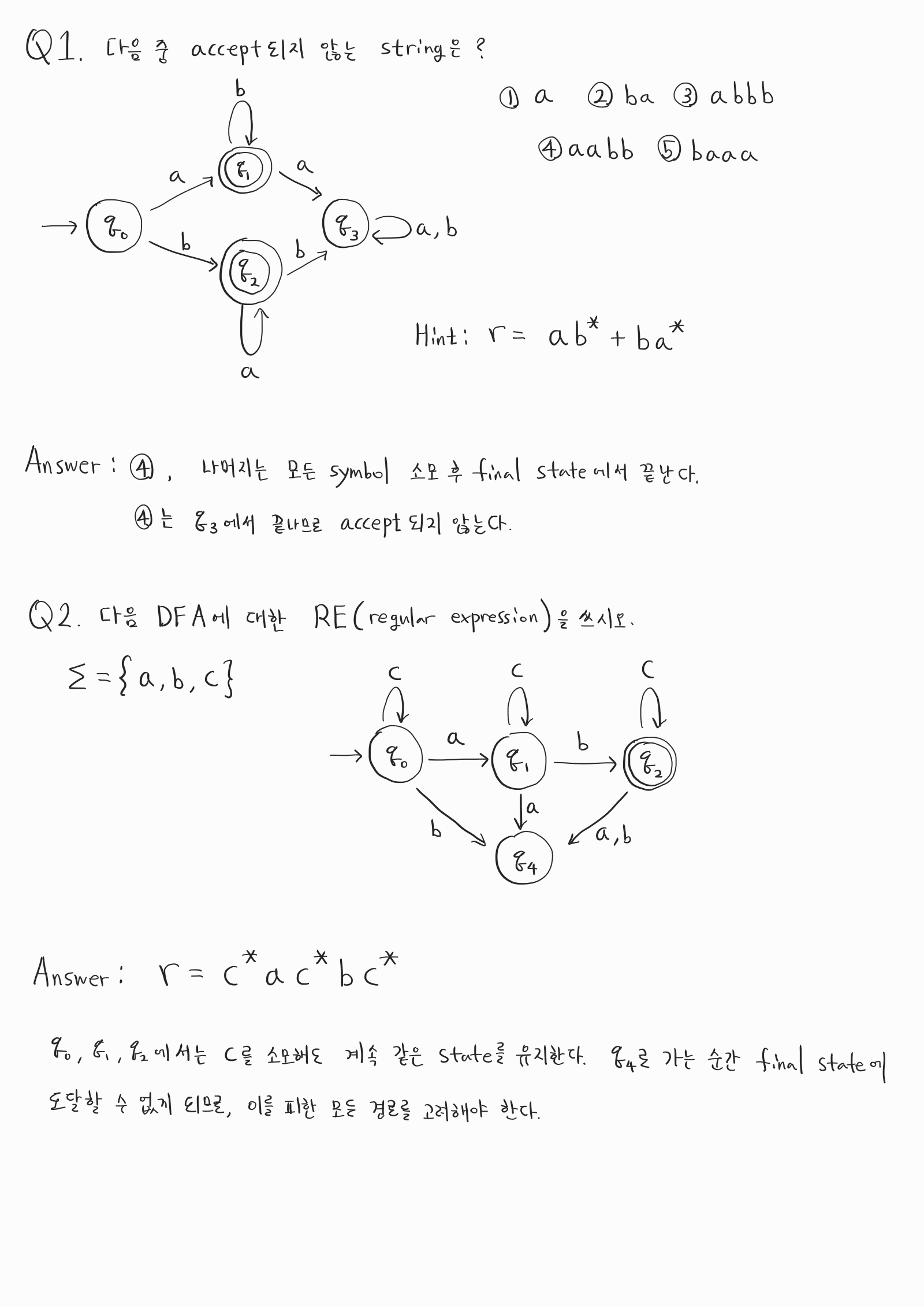
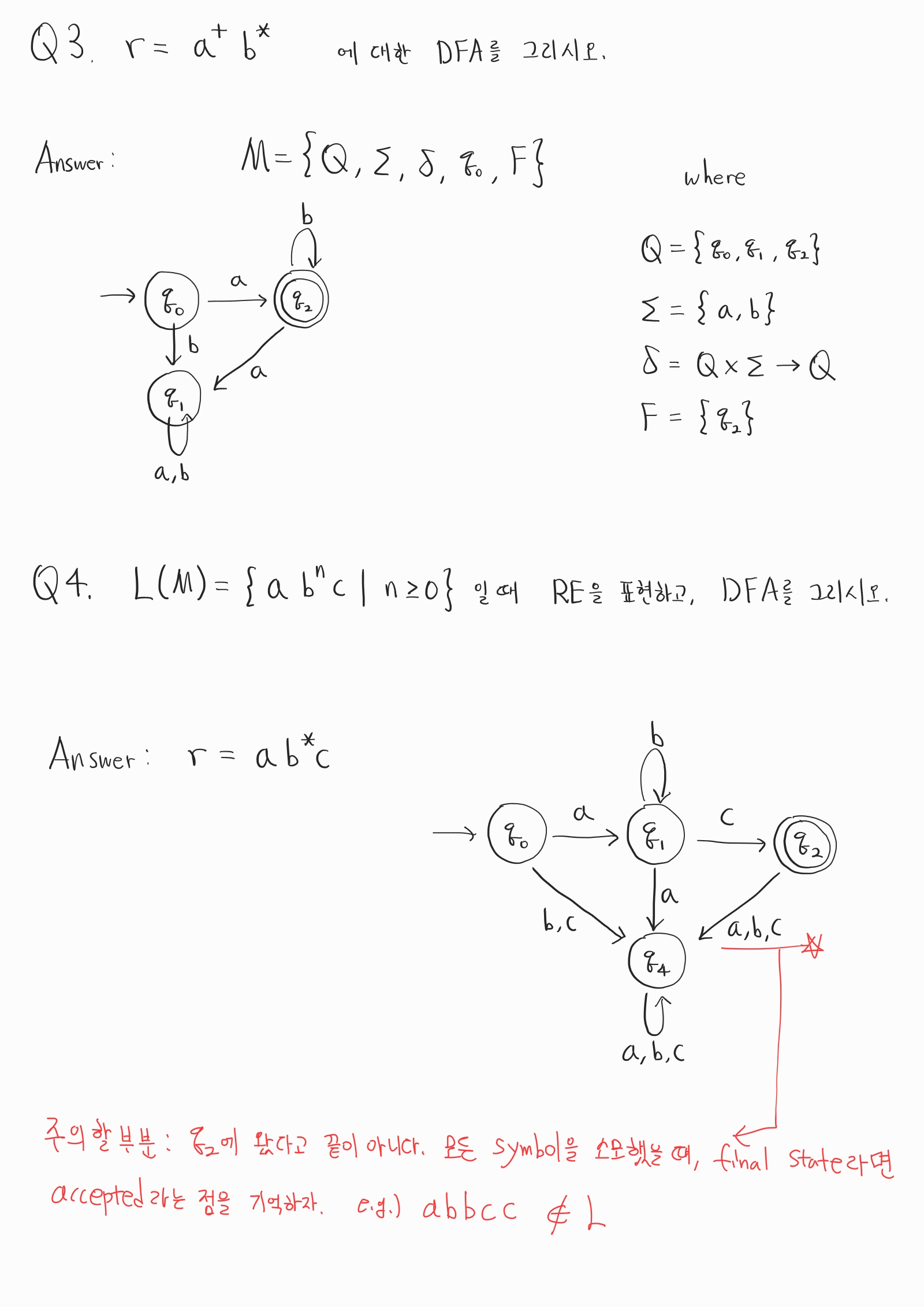
다음 연습 문제를 직접 풀어보시고, 풀이를 보시면서 개념을 이해해보시는 것을 추천합니다.

Regular Expression

위 Example에서 Regular Expression에 대해서 간단히 설명드렸는데요, Language에 속할 수 있는 string을 간단히 나타낸 것을 의미합니다. DFA에 대한 Regular Expression은 반드시 존재합니다. 또한 Regular Expression만 봐도, DFA를 그릴 수 있습니다. 이 부분은 연습이 필요한 부분이므로 아래 연습 문제를 활용하여 만든 연습을 해보시는 것을 추천합니다. 물론 쉽게 하는 방법들이 여럿 존재하지만, 본 포스팅에서는 이 부분에 대해서는 디테일하게 다루지 않겠습니다. Regular Expression을 활용하여 DFA를 그리는 방법은 Arden’s theorem을 참고하시길 바랍니다.
위키백과의 Arden’s Rule 문서

Conclusion

이번 시간에는 간단히 DFA와 Regular Expression에 대해 알아보았습니다. 정말 핵심적인 내용만 간결하게 작성하였기 때문에 설명이 부족하다고 느끼셨을 수도 있을 것 같습니다. 설명이 부족하더라도, 아래 연습 문제를 참고하시면 내용 이해에 어려움은 없을 것이라 믿고 있습니다. 아래의 많은 연습 문제를 풀어보시고, 풀이를 꼭 확인하셔서 이해의 정도를 확인하시길 바랍니다. 이번 강의는 풀이를 자세히 해 놓겠습니다.

Practice