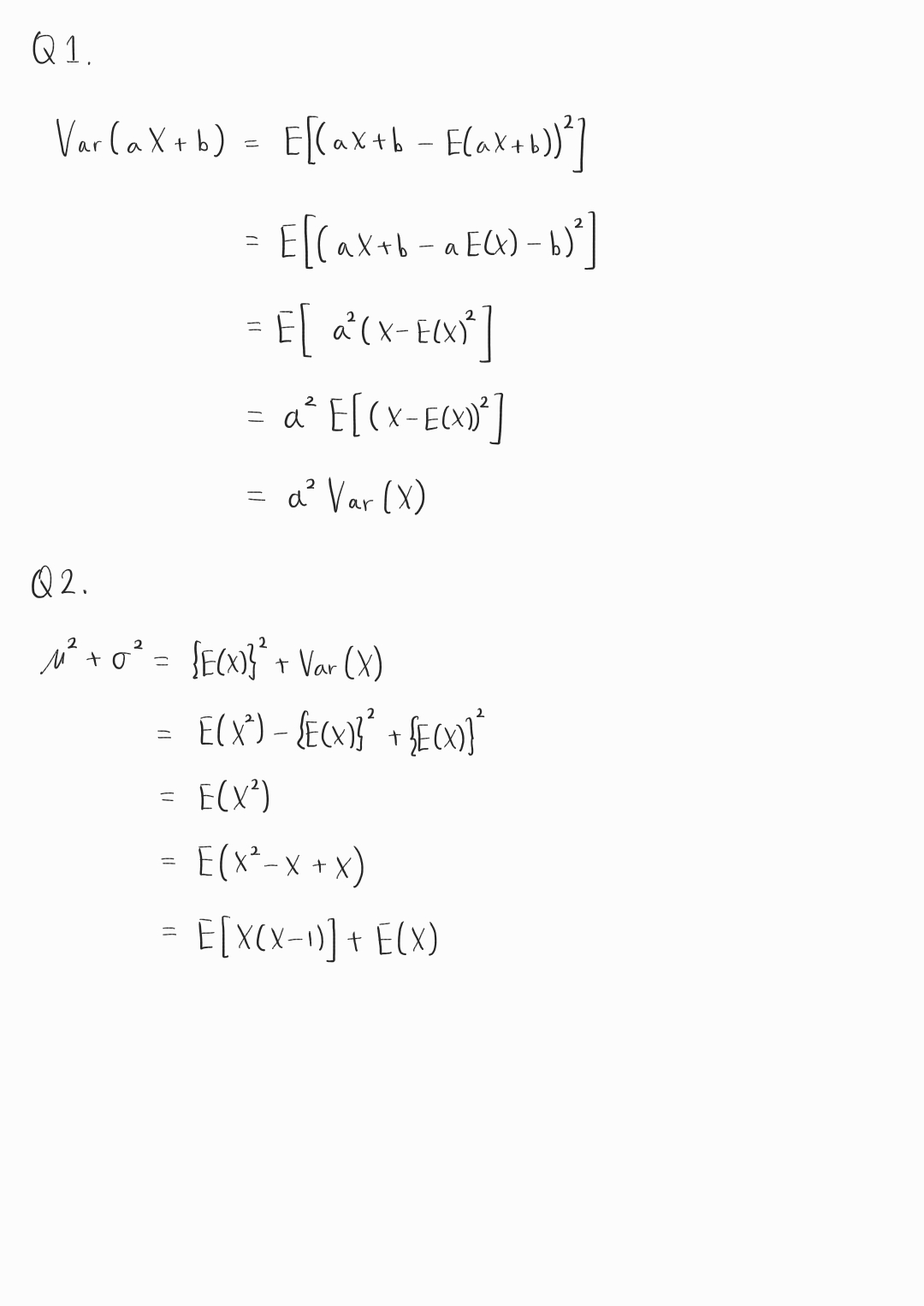[Probabilistics] 확률 이론(5강) - 기댓값, 분산, 표준편차

• 수식이 제대로 보이지 않는다면, 새로고침(F5)을 해주시기 바랍니다.

지난 시간에는 discrete random variable과 continuous random variable에 대해 알아보았습니다.
이번 시간에는 기댓값, 분산, 표준편차에 대해 알아보겠습니다.

Expectation

확률 변수 $g(X)$의 expectation, 또는 mean은 다음과 같이 정의됩니다. 여기서 $f_X(x)$는 pmf 또는 pdf를 의미합니다.

$$ \displaystyle \mathbb{E}[g(X)] = \begin{cases} \displaystyle \int_{-\infty}^{\infty} g(x) f_X(x) \, dx & \text{if } X \text{ is continuous} \\ \displaystyle \sum_{x \in \mathcal{X}} g(x) f_X(x) = \sum_{x \in \mathcal{X}} g(x) P(X = x) & \text{if } X \text{ is discrete} \end{cases} $$

보통 $E(X)$를 많이 구하게 될 텐데요, 여기서 $g(X)=X$라면 $E(X)$의 정의가 됩니다.
추가로, $E|g(X)|=\infty $일 때, $E[g(X)]$는 존재하지 않는다고 합니다.

---

기댓값은 선형성을 만족합니다. 아래는 기댓값에 관한 성질들인데요, 매우 중요하니 증명과 함께 알아두어야 합니다.

• $E[ag(X)]=aE[g(X)]$
  proof:
  $E[ag(X)]=\int_{-\infty }^{\infty }ag(x)f_X(x)dx=a\int_{-\infty }^{\infty }g(x)f_X(x)dx=aE[g(X)]$
  따라서 expection 내부의 상수는 밖으로 뺄 수 있습니다.
  
  
• $E[c]=c$
  여기서 c는 확률 변수가 아닌 그냥 상수입니다.
  proof:
  $E(c)=\int_{-\infty }^{\infty}cf_X(x)dx=c\int_{-\infty}^{\infty}f_X(x)dx=c\times 1=c$
  pdf 전체 구간에 대한 적분 값은 1임을 사용하면 쉽게 증명할 수 있습니다.
  
  
• $E(g_1(X)+g_2(X))=E(g_1(X))+E(g_2(X))$
  proof:
  $E(g_1(X)+g_2(X))=\int_{-\infty}^{\infty}(g_1(X)+g_2(X))f_X(x)dx=\int_{\infty}^{\infty}g_1(x)f_X(x)dx+\int_{-\infty}^{\infty}g_2(x)f_X(x)dx=E(g_1(X))+E(g_2(X))$
  다음과 같이 적분의 성질을 이용하여 간단하게 증명할 수 있습니다.

---

Variance & Standard deviation

이번엔 분산(Variance)에 대해 알아보겠습니다. 분산은 데이터가 평균을 기준으로 얼마나 퍼져 있는지를 나타내는 값입니다. 다음과 같이 정의됩니다.

$$ \displaystyle Var(X)=E[(X-E[X])^2] $$

표준편차(Standard deviation) $\sigma$는 $\sigma=\sqrt{Var(X)}$입니다.

$Var(X)$에 대해 다음이 성립합니다.

• $Var(X)=E(X^2)-{E(X)}^2$
  proof:
  $E(X)=\mu$라고 두겠습니다.
  $Var(X)=E[(X-\mu)^2]=E[X^2-2\mu X+\mu^2]$
  $=E(X^2)-2\mu E(X)+\mu^2=E(X^2)-2\mu^2+\mu^2=E(X^2)-{E(X)}^2$
  
• $Var(aX+b)=a^2Var(X)$
  proof:
  이 증명은 간단하니 연습 문제를 통해 직접 증명해보길 바랍니다.
  

Conclusion

오늘은 expectation, variance, standard deviation에 대해 알아보았습니다. 앞으로도 계속 사용할 개념이므로, 정의 및 관련 성질을 꼭 기억해둡시다.

Practice

Q1. $Var(aX+b)=a^2Var(X)$임을 증명하시오.
Q2. $E(X)=\mu$, $\sigma=\sqrt{Var(X)}$일 때, $\mu^2+\sigma^2=E[X(X-1)]+E(X)$임을 증명하시오.

Answer

정답 보기